Chapter 5 From Idea to Reality: Designing and Building Self-Reproducing Machines in the Mid-20th Century
Alan Turing’s development of a theory of universal computation in the 1930s (Turing, 1937), followed by the appearance of the first digital computers in the 1940s, allowed people to experiment with processes of logical self-reproduction—that is, self-reproduction implemented in software without the extra difficulties entailed by physical self-reproduction. The 1940s and, in particular, the 1950s saw the emergence of the first rigorous theoretical work on the design of self-reproducing machines, and of the first implementations of artificial self-reproducing systems in software (logical self-reproduction) and in hardware (physical self-reproduction).
We have now reached the point where some (but certainly not all) of this work has been widely covered in other publications.62 In this chapter, we review the most significant developments during this period. We begin by looking at John von Neumann’s contributions to the theory of the subject (Sect. 5.1.1); although this is covered in other reviews, we include it because of its significance, because some other reviews do not emphasise von Neumann’s interest in the evolutionary potential of his self-reproducing machines,63 and so that we can present it in the context of what came before and afterwards. We also highlight other work that has not been so widely discussed, such as the pioneering experiments in software evolution by Nils Aall Barricelli (Sect. 5.2.1), Konrad Zuse’s early thoughts about the design and application of self-reproducing machines (Sect. 5.4.2) and Andrei Kolmogorov’s lectures and writing on the subject (Sect. 5.5). Furthermore, while the work of others discussed in this section—such as Lionel Penrose (Sect. 5.3.1) and Homer Jacobson (Sect. 5.3.2)—has been reported elsewhere, we provide some additional technical and biographical details that have not been highlighted in other reviews.
As we mentioned at the start of the book (Sect. 1.3), the work of this period sees the emergence of a third flavour of self-replicator; in addition to continued interest in standard-replicators and evo-replicators, we observe the introduction of the idea that a self-reproducing machine could be used as a general-purpose manufacturing machine—a maker-replicator. This concept was first seen in von Neumann’s work as part of his design theory for self-replicators.
5.1 Theory of Logical Self-Reproduction
The initial development of a theoretical basis for the design of self-reproducing machines in this period was due almost single-handedly to the Hungarian-American scientist John von Neumann in the late 1940s and early 1950s. In the later 1950s and early 1960s there were also contributions from the field of cybernetics, which we summarise in Sect. 5.5. However, these were far less substantial and influential than von Neumann’s work.
5.1.1 John von Neumann (1948)
By the late 1940s, von Neumann (1903–1957) had become interested in developing general principles for the design of immensely complex machines that could tackle pressing scientific and engineering problems. Looking for inspiration in biology, he developed a particular interest in the capacity of biological organisms for self-reproduction, and in the observed evolutionary increase in complexity of some organisms over time. He saw self-reproduction and evolution as a means to an end—to produce complex automata that could solve real problems—rather than an end in itself (von Neumann, 1966, p. 92).
Noting that some processes (e.g. crystal growth) display a trivial kind of self-reproductive ability, von Neumann clarified that the kind of self-reproduction process of interest in his work must have “the ability to undergo inheritable mutations as well as the ability to make another organism like the original” (von Neumann, 1966, p. 86). In other words, an important aspect of his research was the development of design principles for evo-replicators. But his focus was more specific than the design of evo-replicators in general; in addition to being able to evolve, his self-reproducing machines would need the ability to perform other arbitrary operations, and the complexity of these operations should be able to increase each time the machine reproduced, to eventually generate machines capable of solving difficult problems.
By 1948 von Neumann had already proposed a general abstract architecture that might be used to address the problem (von Neumann, 1951).
His solution was inspired by Alan Turing’s work on universal computing machines (Turing, 1937),64 but he modified Turing’s design such that the input and output operations acted upon structures composed of the same materials out of which the machine itself was composed (von Neumann, 1966, pp. 75–76). Von Neumann’s machine could therefore construct other machines as part of its operation.
Von Neumann discussed the level at which the individual parts of the architecture should be defined:
“by choosing the parts too large, by attributing too many and too complex functions to them, you lose the problem at the moment of defining it. … One also loses the problem by defining the parts too small … In this case one would probably get completely bogged down in questions which, while very important and interesting, are entirely anterior to our problem. … So, it is clear that one has to use some common sense criteria about choosing the parts neither too large nor too small.”
John von Neumann, 1949 (von Neumann, 1966, p. 76)
He envisaged a universal construction machine that consisted of three subcomponents: a building unit, a copying unit and a control unit. The building unit, when fed an information tape bearing an encoded description of the design of an arbitrary machine, would build that machine from the description; the copying unit, when fed an information tape, would produce a second copy of the tape; the control unit would coordinate the actions of the other two units.
Von Neumann showed that if this universal construction machine was fed an encoded description of itself, the result was a self-reproducing machine (see Fig. 5.1). The fundamental aspect of the design, which circumvented a potential infinite regress of description, was the dual use of the information tape—to be interpreted as instructions for creating a duplicate machine (by the building unit) and to be copied uninterpreted for use in the duplicate (by the copying unit).65
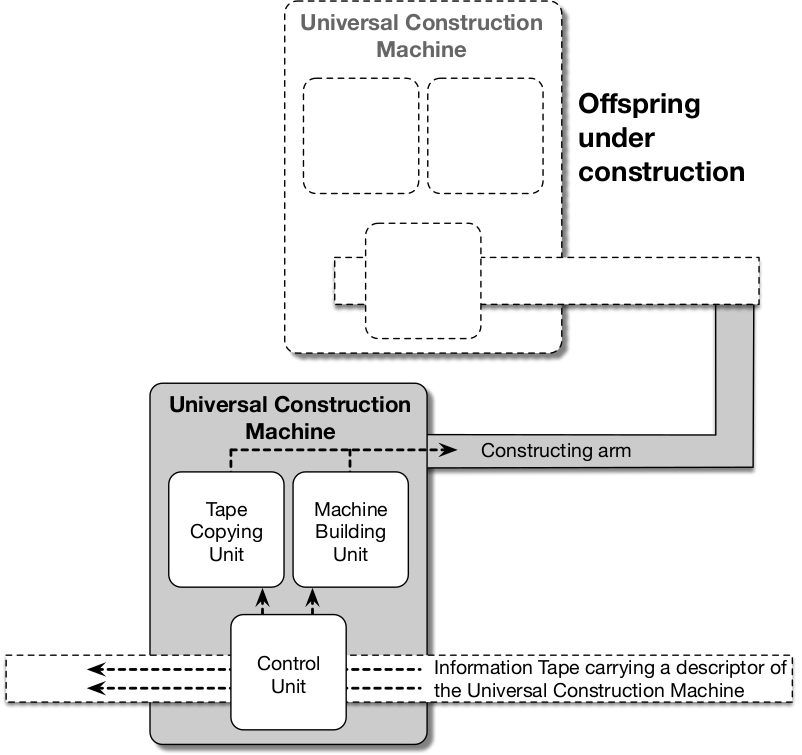
Figure 5.1: Schematic of von Neumann’s design for a universal construction machine capable of self-reproduction and evolution. The machine in the lower part of the image has been supplied with a description of its own design on its information tape. It is shown in the process of using this information to construct a copy of itself and of the information tape, as shown in the upper part of the image.
In addition to self-reproduction, the design also satisfied von Neumann’s requirement that the machines should be able to perform other tasks of arbitrary complexity.
He showed how such machines could produce offspring capable of performing more complex tasks than their parents, and how such increases in complexity could come about through heritable mutations to the information tape. Hence, these kinds of machines have the potential to participate in an evolutionary process leading to progressively more complex machines which could perform arbitrary tasks in addition to self-reproduction.
To summarise, it was von Neumann’s desire to create self-reproducing machines that could perform arbitrary useful tasks in addition to reproduction (where the complexity of these tasks could increase over the course of evolution), coupled with his inspiration from Turing’s idea of a universal computing machine, which drove him to the idea of a self-reproducing universal construction machine—a maker-replicator (and indeed an evolvable maker-replicator, or evo-maker-replicator).
Having established a general theory of the logical design of an evo-maker-replicator, von Neumann planned to explore the topic experimentally with the aid of a series of models (Aspray & Burks, 1987, pp. 374–381). 66 The first of these was the so-called “cellular model” based upon a simple two-dimensional grid of squares (cells) in which, at any given time, each square could be in one of a small number of possible states.67 The other models had been planned to progressively move away from discrete models to ones with more “lifelike” properties such as continuous dynamics and probabilistic operation. Von Neumann emphasised that the design of the machines would depend critically upon the nature of their environment: “it’s meaningless to say that an automaton is good or bad, fast or slow, reliable or unreliable, without telling in what milieu it operates” (von Neumann, 1966, p. 72). Studying self-reproduction in a series of progressively more complex environments was therefore a sensible approach.
Before his early death in 1957, von Neumann was only able to produce a detailed design for the first of these, the cellular model. Despite the ingenuity of the design, to actually implement it on a computer was far beyond the available computational power of the time. Just a single machine and information tape bearing an encoded description of the machine would require approximately 200,000 cells (Kemeny, 1955, p. 66); to simulate the production of just one offspring would require at least double that number. Indeed, the first implementation of the cellular model (with some simplifications) did not appear for another forty years (Pesavento, 1995), followed by several more recent versions—an example is shown in Fig. 5.2.
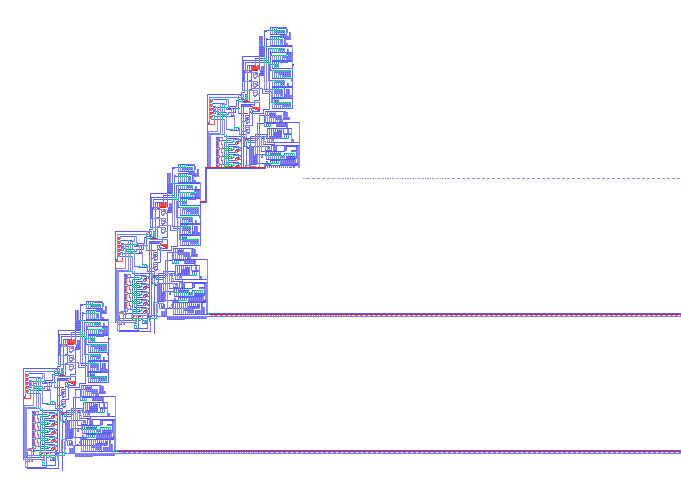
Figure 5.2: Image from a recent full implementation of a self-reproducing automata based upon von Neumann’s design. This version, from 2008, employs Renato Nobili and Umberto Pesavento’s universal constructor design with tape design by Tim Hutton, and is implemented in the Golly cellular automata software.
Von Neumann’s ideas soon spread beyond the scientific community, and by the mid-1950s they were the topic of articles in popular science magazines (e.g. (Kemeny, 1955)68). However, despite its very substantial achievements, the work only partially addressed the problems involved in designing physical self-reproducing machines. In particular, the work did not address issues regarding fuel and energy, nor did the architecture include any kind of self-maintenance system—the basic machine as presented would be very susceptible to any kind of external damage from the environment. We return to these issues of extending von Neumann’s design to handle real-world self-reproduction in Sect. 7.3.1.
The universal construction machine is like a massively complex Lego kit where the instruction manual is also built from Lego, and where the kit can read, execute and copy the manual itself. How such a kit might originally come about was not part of the problem addressed by von Neumann. However, if such a kit did exist, then it could operate and evolve purely on a diet of elementary Lego bricks—the complexity of its operation is due mostly to the organisation of the machine and to the information contained in the instruction manual, rather than the individual bricks. We will return to the question of origins—of how complex self-reproducing systems might arise in an environment in the absence of an original designer—in Sect. 7.3. Von Neumann restricted himself to the following remarks on the topic:
“… living organisms are very complicated aggregations of elementary parts, and by any reasonable theory of probability or thermodynamics highly improbable. That they should occur in the world at all is a miracle of the first magnitude; the only thing which removes, or mitigates, this miracle is that they reproduce themselves. Therefore, if by any peculiar accident there should ever be one of them, from there on the rules of probability do not apply, and there will be many of them, at least if the milieu is reasonable. But a reasonable milieu is already a thermodynamically much less improbable thing. So, the operations of probability somehow leave a loophole at this point, and it is by the process of self-reproduction that they are pierced.”
John von Neumann, 1949 (von Neumann, 1966, p. 78)
Freeman Dyson, whose contributions to the subject we discuss in Sect. 6.3, summarised the significance of von Neumman’s work as follows:
“Von Neumann believed that the possibility of a universal automaton was ultimately responsible for the possibility of indefinitely continued biological evolution. In evolving from simpler to more complex organisms you do not have to redesign the basic biochemical machinery as you go along. You have only to modify and extend the genetic instructions. Everything we have learned about evolution since 1948 tends to confirm that von Neumann was right.”
Freeman Dyson, 1979 (F. Dyson, 1979, p. 196)
Von Neumann’s contribution to the theory of self-reproducing machines has been hugely influential in later work on the topic. We provide an overview of these more recent developments in Chap. 6.
5.2 Realisations of Logical Self-Reproduction
Beyond von Neumann’s development of a theoretical basis for the the design of evo-maker-replicators, the 1950s also saw the first work in actually building artificial self-reproducing machines, both in software and hardware. These projects took a very different approach to the subject, building standard-replicators or evo-replicators using simple elementary units that could combine to form self-reproducing configurations. In contrast to von Neumann, the authors of these projects were motivated (at least in part) by questions concerning the origin of life on Earth.
5.2.1 Nils Aall Barricelli (1953)
The story of Nils Aall Barricelli (1912–1993) is remarkable in many ways. To summarise what we will discuss below, in 1953 he became the first person to perform experiments in logical self-reproduction and artificial evolution on computers. His interest in achieving ongoing, open-ended evolution of progressively more complex digital organisms, and his conviction that he was instantiating, rather than merely simulating, evolutionary processes in a computational medium, place his research firmly within the present-day scientific discipline of Artificial Life.69 Yet, despite his pioneering achievements, he is still relatively unknown even within the contemporary ALife community, where he might justifiably be regarded as one of the founding fathers of the field.70
Born in Rome to an Italian father and Norwegian mother, Barricelli moved to Norway in 1936 at the age of 24.71 He took up a lecturing position in physics at the University of Oslo, although he maintained a wide range of academic interests throughout his life. By the late 1940s, he had become interested in the theory of symbiogenesis, introduced in the early twentieth century by the Russian botanists Konstantin Merezhkovsky and Boris Kozo-Polyansky (Kozo-Polyanski, 1924), (Kozo-Polyanski et al., 2010). According to this theory, “the genes [of a cell] … spring from originally independent virus or virus-like organisms” (Barricelli, 1963, p. 74).
Having performed some initial simulation experiments of the theory by hand on graph paper, Barricelli saw the potential for running greatly expanded experiments on an electronic computer. He successfully applied to join von Neumann’s group at the Institute for Advanced Studies in Princeton as a visiting researcher, where he would have access to the group’s recently-built computer, the “IAS Machine.” Upon his arrival in January 1953, Barricelli worked night-shifts when the machine was free from its daytime employment on national defence-related work. He conducted a series of experiments in 1953 and during subsequent return visits in 1954 and 1956 (Barricelli, 1962, p. 88).
Barricelli was interested in studying the simplest possible systems that could display evolutionary processes leading to “the formation of organs and properties with a complexity comparable to those of living organisms” (Barricelli, 1962, p. 73). He therefore assumed that the individual elements in his systems were already equipped with some capacity for self-reproduction. This was in sharp contrast to von Neumann’s work, which aimed to understand how that capacity might be built into a system composed of individual elements that were not themselves self-reproducing. We will discuss the difference between these two approaches in more detail in Sect. 7.3.
Barricelli’s experiments were conducted in a virtual one-dimensional world—a strip of discrete square units updated in discrete time steps. Each square in the world could either be empty (represented by the value 0) or occupied by a small positive or negative non-zero integer.72 The state of a square at the next time step was determined by its state at the current time step together with the state of its neighbours. The exact details of this mapping were determined by the system’s update rule.
By exploring a series of different update rules, Barricelli observed the emergence of progressively more complex forms of behaviour.73 His earliest hand-drawn simulation experiments involved update rules that implemented what he described as the bare necessities of a Darwinian evolution process, such that individual numbers in his one-dimensional world were (1) self-reproducing and (2) capable of undergoing heritable mutation (Barricelli, 1962, p. 71). Specifically, if a square contained a non-zero integer n at time t, then at time t+1 the same integer n would also be copied into the square n places to the left or right of the original, depending on whether it was positive or negative. If two integers tried to reproduce into the same square, then a different integer was placed in the square, thereby introducing a mutation into the system (Barricelli experimented with various rules for deciding what the mutated integer should be).
Although the system was capable of reaching a stable state through a “process of adaptation to the environmental conditions” (Barricelli, 1962, p. 72), Barricelli was unsatisfied with the end result: “No matter how many mutations occur, the numbers … will never become anything more complex than plain numbers” (Barricelli, 1962, p. 73). It was apparent that something more was required beyond the basic Darwinian properties of reproduction and heritable mutation.
![Examples of (a) emergence and (b) self-reproduction of a symbioorganism in Barricelli’s system described in (Barricelli, 1962). Each row in these figures represents the state of the one-dimensional world at a given time. Each successive time-step of the system is plotted below the last, so the figure shows time advancing from the top to the bottom of the plot. The symbiogorganism that emerges in (a) is [5,-3,1,-3, ,-3,1]. The same symbioorganism is then used to seed the system in the top row of (b). The update rules used in these examples are as follows: (1) Each number n is moved to a position n squares to the right (if n is positive) or n squares to the left (if n is negative) in the next row; (2) If a collision occurs between two different numbers in the new row, the square remains empty—this is indicated by the star symbols in the second row of (a); (3) If a collision occurs between two identical numbers, that number is written once to the square only; (4) If the new number n lands in a square which has another number m directly above it in the preceding row, a second copy of n is produced m squares to the right (if m is positive) or to the left (if m is negative) of the position of the original n (this rule can be iterated if the second copy of n also lands in a square with another number directly above it).](images/barricelli-output-figs.png)
Figure 5.3: Examples of (a) emergence and (b) self-reproduction of a symbioorganism in Barricelli’s system described in (Barricelli, 1962). Each row in these figures represents the state of the one-dimensional world at a given time. Each successive time-step of the system is plotted below the last, so the figure shows time advancing from the top to the bottom of the plot. The symbiogorganism that emerges in (a) is [5,-3,1,-3, ,-3,1]. The same symbioorganism is then used to seed the system in the top row of (b). The update rules used in these examples are as follows: (1) Each number n is moved to a position n squares to the right (if n is positive) or n squares to the left (if n is negative) in the next row; (2) If a collision occurs between two different numbers in the new row, the square remains empty—this is indicated by the star symbols in the second row of (a); (3) If a collision occurs between two identical numbers, that number is written once to the square only; (4) If the new number n lands in a square which has another number m directly above it in the preceding row, a second copy of n is produced m squares to the right (if m is positive) or to the left (if m is negative) of the position of the original n (this rule can be iterated if the second copy of n also lands in a square with another number directly above it).
For Barricelli, the symbiogenesis theory potentially supplied the missing ingredient. He made changes to the update rules for his one-dimensional world such that each number could only reproduce with the support of a “helper” number in a specific nearby location. The helper would also dictate the location into which the number reproduced. In this way, reproduction in the system was no longer at the level of “plain numbers”: if it was to happen in a sustained manner, it now required the mutual co-operation of spatially organised aggregates of numbers. Barricelli did indeed see such aggregates emerge, and called them “numerical symbioorganisms” (Barricelli, 1962, p. 80).74 His subsequent experiments on the IAS Machine were devoted to studying their properties. Among the general properties observed in the symbioorganisms,75 Barricelli gave examples of the following: self-reproduction, crossing, great variability, mutation, spontaneous formation, parasitism, repairing mechanisms and evolution (Barricelli, 1962, pp. 81–88) (see Fig. 5.3).76 In evolution experiments which ran for thousands of generations, successions of various dominant species of symbioorganism were seen to emerge (see Fig. 5.4).77 Barricelli also performed competition experiments where he pitted some of the successful species of symbioorganisms that evolved during the runs against each other. The results led him to conclude that “it is clear that the ability to survive is improved by evolution” (Barricelli, 1962, p. 92). He also noted that the phenomenon of crossing of genetic material between different symbioorganisms appeared at an early stage in all of his experiments, and remarked that “[t]he common idea that living beings may have existed for a long time before crossing mechanisms appeared is hardly consistent with a symbiogenetic interpretation” (Barricelli, 1962, p. 93).
Having observed in his competition experiments that the symbioorganisms could exhibit evolutionary improvements, Barricelli wondered “whether it would be possible to select symbioorganisms able to perform a specific task assigned to them” (Barricelli, 1963, p. 100). To investigate this question, he ran a further set of experiments on an IBM 704 computer78 at the A. E. C. Computing Center at New York University in 1959 and 1960 (Barricelli, 1963, p. 107).

Figure 5.4: A sample output from a modern reimplementation of Barricelli’s symbioorganism experiments written by Alexander Galloway. Each horizontal strip of the image represents the state of the one-dimensional world at a given time. Each successive time-step of the system is plotted below the last, so the figure shows time advancing from the top to the bottom of the plot. The different colours represent different symbioorganisms, and their rise and fall over time can be seen in the expanding and contracting patterns they create in the plot.
The new experiments involved a relatively small conceptual change—if two numbers tried to copy themselves into the same memory location, rather than causing a mutation as in the original experiments, the rival symbioorganisms would now compete in a game where the result would determine which one was allowed to occupy the contested location. The game chosen was Tac Tix,79 and Barricelli devised a method for interpreting a specific consecutive sixteen number sub-sequence of a symbioorganism as a strategy for playing it (Barricelli, 1963, pp. 103–106). The symbioorganisms’ new-found ability to perform other tasks as well as reproduce was one they shared with von Neumann’s theoretical architecture—although Barricelli’s design was much more basic, involving a fixed interpretation of the numbers as a strategy for a specific game, in contrast to von Neumann’s interpretation machinery which was itself able to evolve and which formed a component of a universal construction machine.
After some experimentation, the 1960 experiments yielded several runs in which an evolutionary improvement was observed in the fraction of symbioorganisms playing the game at a non-zero skill level.80 Although the results were not consistent across runs, and in at least one of the reported runs a parasite evolved which disrupted the further improvement of the host,81 Barricelli summarised the significance of the results as follows:
“… the value of the results presented does not primarily rest on the possibilities for practical applications, but on their biotheoretical significance. … It has been shown that given a chance to act on a set of pawns or toy bricks of some sort the symbioorganisms will `learn’ how to operate them in a way which increases their chance for survival. This tendency to act on any thing which can have importance for survival is the key to the understanding of the formation of complex instruments and organs and the ultimate development of a whole body of somatic or non-genetic structures.”
— Nils Aall Barricelli, 1963 (Barricelli, 1963, p. 117)
In addition to the preceding remarks about the fixed mechanism for interpreting a symbioorganism’s game strategy, it has recently been argued that the approach of introducing a predefined game to be played restricted the open-ended evolutionary potential of the system by “flattening complex interactions back into linear causal chains” (Galloway, 2012, p. 41). In other words, the game was not co-evolving along with the organisms. Barricelli himself seems to have been sensitive to these criticisms, and in his final published work in the area in 1987 he sets out some suggested modifications to his original design whereby symbioorganisms have the opportunity to evolve operational elements such as membrane-like structures (Barricelli, 1987).82 Such elements would allow the symbioorganisms to control their local environment and thereby improve their chances of survival and reproduction in a way that operated within the general laws of the world instead of via a special-case predefined game to be played. He discussed how a more pronounced genotype–phenotype distinction would emerge in such a system, accompanied by what could be regarded as a “genetic language” to specify a symbioorganism’s operational elements and their organisation (Barricelli, 1987, pp. 143–144). At the age of 75, Barricelli was clearly not intending to commence a new line of experimental work himself, and the paper was written as a set of suggestions for a future programmer to follow.83 He died six years later in 1993, at the age of 81.
5.3 Realisations of Physical Self-Reproduction
The first publications describing implementations of physical self-reproducing systems appeared just a few years after Barricelli’s initial work on software-based (logical) self-reproduction. The two most significant authors of work on early hardware-based self-reproduction are Lionel Penrose and Homer Jacobson. Both of their projects followed Barricelli’s approach; they employed systems in which the elementary units are contrived such that particular compound chains of units can catalyse the formation of further copies of the same compound. These chains, which can be very short, can therefore reproduce without the complexity of von Neumann’s design. While Barricelli had successfully demonstrated the first implementation of evo-replicators in software, Penrose and Jacobson’s physical implementations focused on simple standard-replicators; although, as we describe below, they both discussed how their models could be further extended to improve their evolutionary potential.
5.3.1 Lionel Penrose (1957)
Lionel Penrose (1898–1972) was a distinguished British scientist best known for his work in human genetics and intellectual disability (Harris, 1973). His interests within these fields were broad, and he published on many topics beyond his core research. Over the period 1957–1959, Penrose produced three papers describing a series of designs of self-reproductive chains of mechanical wooden units (Penrose & Penrose, 1957), (Penrose, 1958), (Penrose, 1959).84 His aim was to investigate very simple forms of self-reproduction that could potentially have been employed by the earliest forms of life on Earth. As his son Roger recalls, “[o]ften he illustrated his scientific ideas by means of working models. … Frequently these models would be aids to clarifying his own thoughts as much as demonstrations for others. But there is no doubt that a major influence in driving him on in this direction was his sense of fun and sheer enjoyment in constructing things from wood and other materials” (Harris, 1973, p. 545).
For the purposes of these models, Penroseprovided the following definition of self-reproduction:
“A structure may be said to be self-reproducing if it causes the formation of two or more new structures similar to itself in every detail of shape and also the same size, after having been placed in a suitable environment.”
— Lionel Penrose, 1958 (Penrose, 1958, p. 59)
He did not restrict his investigation to cases of non-trivial self-reproduction in von Neumann’s sense (i.e. to systems capable of an evolutionary increase in complexity via heritable mutations). However, he did set out certain standards to guide his work: that the elementary units of the system “must be as simple as possible”; that there “must be as few different kinds [of unit] as possible”; and that the units “must be capable of forming at least two (preferably an unlimited number) of distinct self-reproducing structures” (Penrose, 1959, p. 106). One further restriction was that a self-reproducing structure could only be built by copying a previously existing seed structure, i.e. there could be no spontaneous generation of self-reproducing structures. The logic for this final restriction was the fact that spontaneous generation was not observed in biological life (Penrose, 1959, p. 106).85
The first paper described a simple system comprising multiple copies of two basic types of wooden block. The two types (which we will refer to as A and B) look deceptively simple, but were cleverly designed so that, when in a particular orientation, an A unit and a B unit could hook together in two distinct ways (A-B or B-A), as shown in Fig. 5.5.

Figure 5.5: Penrose’s simple two-unit model showing replication of an introduced B-A seed unit (middle) and of an introduced A-B unit (bottom). A description of the system is provided in (Penrose & Penrose, 1957).
The units were restricted to move along a horizontal channel of limited height such that they could not pass one another. In this system, if a collection of individual A and B units were randomly placed in the channel and the channel was shaken horizontally, the units would collide but would never link together. However, if a single A-B linked unit was placed in the channel before the channel was shaken, it acted as a “seed”. The seed caused individual units colliding with it to assume the correct orientation to form further linked A-B units. The same result occurred with an initial B-A seed too, but the reproduction always bred true to the initial seed.
This first design served as a demonstration of how physical self-reproduction could be implemented with an extremely simple mechanism. From the experience gained with this design, Penrose identified five principles of self-reproduction which guided his later work (Penrose, 1958, pp. 61–62). In contrast to von Neumann’s work on the logical design of self-reproducing machines, Penrose’s principles very much focused on physical and energetic concerns: (1) The units must each have at least two possible states, one of which is a neutral state (in which potential energy is lowest) and other states which are associated with various degrees of activation; (2) In order to form a self-reproducing structure, kinetic energy must be captured and stored as potential energy in its constituent units (hence the constituent units are activated); (3) The activated structure or machine must have definite boundaries (unlike a crystal, for example); (4) Each activated unit must be capable of communicating its state to another unit with which it is in close contact; and (5) The chances of units becoming attached correctly can be increased by guides (or tracks, channels, etc.), which act like catalysts. These guides could be in the environment (as in the simplest system described above) or could be part of the units themselves (e.g. interlocking edges).
From this starting point, the later papers (Penrose, 1958), (Penrose, 1959) described a series of progressively more complicated models. The most complicated schemes that Penrose devised and built were inspired by the way DNA strands are copied through a process of template reproduction by base pairing (see (Penrose, 1958, pp. 109–114) and (Penrose, 1959, pp. 68–71)). The elementary units of these schemes were hybrids of an elaboration of the simple self-catalysing pairs of A and B units from Penrose’s simplest model (which acted as the “base pairs”), together with a system of guides, passive hooks and activation and release mechanisms. These additional features allowed the formation of linear chains of units of arbitrary length and promoted the coordinated sequence of associations and disassociations required for the chains to reproduce. A schematic showing the operation of one of these more complex designs, with handwritten annotations by Penrose, is shown in Fig. 5.6. Photographs of his physical implementation of another of his more complex designs are shown in Fig. 5.7.

Figure 5.6: Handwritten annotated schematic of one of Penrose’s designs for a linear-chain replicator (from the Wellcome Library archive).
Penrose discussed how self-reproducing structures in a system like this might perform other actions in their environment beyond self-reproduction, dependent upon their configuration. Such functions could be subject to natural selection, he argued; moreover, mutations and recombinations could occur, allowing the structures to participate in an evolutionary process—becoming evo-replicators rather than just standard-replicators (Penrose, 1959, pp. 112–114).

Figure 5.7: Photographs demonstrating successive stages of replication in Penrose’s physical implementation of one of his more complex self-reproduction schemes. The original four-unit seed replicator is shown in the center of (a), surrounded by four individual food units. Over (b)–(e) the food units attach to the seed in the correct places to form two copies of the original seed (e), which separate once formed (f).
Echoing the statements made by Barricelli about the ontological status of his symbioorganisms, Penrose stated that his designs were not theoretical models but self-reproducing machines in their own right (Penrose, 1959, p. 114).86 He argued that they demonstrated that self-reproduction and evolution could happen in relatively simple systems, and that work such as this could help us in understanding the early evolution of life on Earth before the emergence of complex DNA-based reproduction. The relationship between his self-reproducing machines and biological self-reproduction was further explored in subsequent publications (e.g. (Penrose, 1960), (Penrose, 1962)).
Two films were produced showing Penrose demonstrating his various models.87 The first, entitled “Automatic Mechanical Self-Replication”, was made in 1958 and shown at the Tenth International Congress on Genetics in Montreal, and the second, “Automatic Mechanical Self-Replication (Part 2)”, which shows the most advanced models, was made in 1961 and shown at the Institute of Contemporary Arts in London. These films are shown below.
Penrose’s work attracted widespread attention at the time. In addition to presenting numerous academic lectures and demonstrations on the topic,88 one of the articles referred to above was published in the popular science magazine Scientific American (Penrose, 1959). Furthermore, Penrose appeared in an episode of the BBC TV series Science International in December 1959, which had a special feature on the topic “What is Life?”, 89 and his original simple self-reproducing units were also manufactured and sold by the cybernetics organisation Artorga for demonstration and education purposes to universities, schools and individuals.90 Reporting on the presentation of the first film at the Tenth International Congress on Genetics, the Montreal Gazette voiced fears that such work might potentially lead to an artificial self-replicator that got “out of control” and declared that “[t]he implications of this work are tremendous—and a little terrifying” (Cahill, 1958).
5.3.2 Homer Jacobson (1958)
At around the same time as Penrose’s publications, Homer Jacobson (1922–), a chemistry professor at Brooklyn College in New York, published details of a quite different hardware implementation of self-reproduction (Jacobson, 1958). He suggested that the real value of this kind of model was to “call attention to the abstract functions inherent in the processes they represent” (Jacobson, 1958, p. 264).
The paper began by setting out what Jacobson described as the “obvious essentials in any reproducing system.” These were (1) “An environment, in which random elements, or parts, freely circulate”; (2) “An adequate supply of parts”; (3) “A usable source of energy for assembly of these parts”; and (4) “An accidentally or purposively assembled proto-individual, composed of the available parts, and synthesizing them into a functional copy of its own assembly, using the available energy to do so” (Jacobson, 1958, p. 255).
While this list of requirements is fairly close to Penrose’s assumptions, Jacobson was clearly thinking of a somewhat more complex, electromechanical setting for his work. He suggested that the minimum set of part types necessary to build such a system would include (1) an energy transducer, (2) an information storage medium containing some kind of plan for assembly of an organism, and (3) some kind of sensory system (Jacobson, 1958, p. 255).
The implementation was based upon a model railway track, around which two types of specially adapted locomotive cars circulated.
In the simplest version described in the paper, the track was oval and featured a number of sidings. Type A cars were equipped with electromechanical machinery inspired by the punch card, and stored the instructions necessary to direct the reproduction of a seed “organism”. Type B cars were equipped with devices both for controlling points on the track (which determined whether passing cars would continue on the main track or be diverted to a siding) and for sensing if a car was nearby, and if so, of what type.
The self-reproduction process was initiated by placing a seed organism on one of the sidings. This comprised two connected cars, a type A car at the front with a type B car behind. Communicating with each other to coordinate their actions, the A and B cars of the seed organism picked out single A and B cars as they passed by on the main track, and controlled the points to create a replica two-car organism on an adjacent siding.
Jacobson successfully designed and implemented a working version of this system, with full details given in the paper. He also described some possible extensions to the system, including versions where the seed could produce more than one offspring, where the organisms could lay their own points and sidings, where the information on the organism’s punch card was copied during the reproduction process rather than pre-existing in the individual A cars,91 and where the constituent cars of “dead” (dormant) organisms could be recycled for use in further rounds of reproduction. Jacobson provided notes (in varying degrees of detail) on how these features might be implemented in theory, although the complexities involved meant that they remained unimplemented in practice.92
The paper includes a discussion of the complexity of the system’s parts, in which Jacobson notes that “living beings are complex assemblies of simple parts, while the models are simple assemblies of complex parts” (Jacobson, 1958, p. 264). He admitted that reproduction in his models relied upon the detailed properties of an “extremely arbitrary” environment (he viewed the environments in von Neumann’s proposed models of self-reproduction as equally arbitrary), and that their “unnatural (i.e. artifactual) quality” makes them uncomfortable for biologists to accept. In other words, the design of the basic parts and dynamics of these environments was not guided by any fundamental physical principles but rather by the specific intention of allowing particular structures to reproduce. He suggested that models such as these could perhaps be “rated as to an elegance factor which increases as the environment is made simpler, with less built-in instrumentation, and simpler parts” (Jacobson, 1958, p. 263).
The discussion ended with some consideration of the application of information theory to compare the informational capacity of the model system to estimates of the informational capacity of minimal forms of biological life.93 These considerations led Jacobson to conclude that “[his] models, information theory, and thermodynamics all seem to agree that the probable complexity of the first living being was rather small” (Jacobson, 1958, p. 268).
The year after Jacobson’s paper appeared, Harold Morowitz published a brief letter in the same journal in which he described a simple electromagnetic self-reproducing system comprising two distinct types of part floating in water (Morowitz, 1959). Morowitz cites Jacobson as his inspiration, although some aspects of his design are closer to Penrose’s approach.
5.4 Scientific Speculation in the 1950s
In addition to advances in theory and working models, the 1950s also saw continued speculation on the longer-term applications and impact of artificial self-reproducing systems. Some relevant work from science fiction was already discussed in Sect. 4.1.3. Beyond this, we now look at speculative work by scientists during this period.
5.4.1 Edward F. Moore (1956)
Perhaps the most notable speculation on applications of self-reproducing systems from the scientific literature of the 1950s can be found in a Scientific American article by the American mathematician Edward F. Moore (1925–2003). Taking von Neumann’s work as a starting point, it proposes a research programme to design and build much more ambitious self-reproducing machines. In addition to self-reproduction, Moore’s machines would be able to produce materials of economic value, which could then be harvested with exponentially increasing yields (E. F. Moore, 1956). His interests were therefore squarely on the potential of self-reproducing machines as maker-replicators. Moore introduced his proposal by explaining:
“I would like to propose [a] self-reproducing machine, more complicated and more expensive than Von Neumann’s, which could be of considerable economic value. It would make copies of itself not from artificial parts in a stock room but from materials in nature. I call it an artificial living plant. Like a botanical plant, the machine would have the ability to extract its own raw materials from the air, water and soil. It would obtain energy from sunlight … It would use this energy to refine and purify the materials and to manufacture them into parts. Then, like Von Neumann’s self-reproducing machine, it would assemble these parts to make a duplicate of itself.”
— Edward F. Moore, 1956 (E. F. Moore, 1956, p. 118)
The proposal outlined the general aims and challenges of the research programme, with rough estimates of overall time and costs. If sufficient effort was deployed on the project, Moore thought that 5–10 years and $50–70m would be sufficient in the best case, extending to several decades and hundreds of millions of dollars if things did not go so smoothly.
Moore envisaged the machines being constructed from electromechanical parts, rather than biochemical components, because of our better understanding of their design principles. The idea was that these artificial plants would be most useful in currently uncultivated locations, starting in areas such as seashores with relatively easy access to materials and sunlight, and potentially moving to more challenging environments such as the ocean surface, deserts and the continent of Antarctica.
Noting that von Neumann had already solved the problem of the logic of self-reproduction, Moore discussed other difficulties, arguing that the necessary chemical engineering would present the greatest challenges. Reasoning that the energy requirements of manufacture would scale with machine mass, and yet energy capture from sunlight would only scale with surface area, he envisaged “small, or at least very thin” machines (E. F. Moore, 1956, p. 121). These would need to be equipped with “wheels or a propeller” to enable offspring to spread and avoid overcrowding (E. F. Moore, 1956, p. 124).
Moore identified the most important general criterion for success as reproduction time (such as the time required for a population of artificial plants to double in number) and suggested that to be economically sensible, this would need to be at the very least faster than “the time it takes for money to double at compound interest” (E. F. Moore, 1956, p. 121). No doubt wisely, he suggested that such a machine should not be endowed with evolutionary abilities, “lest it take on undesirable characteristics” (E. F. Moore, 1956, p. 122).
The article ended with some brief discussion of potential problems from perspectives of ecology, economics and society—although the one sentence given to potential ecological problems leaves plenty of scope for further elaboration.
5.4.2 Konrad Zuse (1957)
A year after Moore’s article appeared, the German computer pioneer Konrad Zuse (1910–1995) published his first paper on the subject of machine self-reproduction (Zuse, 1957). The article was an extract from a lecture he presented at the Technical University of Berlin on 28 May 1957 on the occasion of being awarded an honorary doctorate.94 Whereas von Neumann had developed the subject from a theoretical perspective, and Moore had proposed advanced uses of the technology but left the implementational details to be addressed in a future research programme, Zuse wished to approach the problem of self-reproduction from the perspective of practical realisation: “To me the practical problems involved in this concept are the actual bottlenecks that must be conquered” (Zuse, 1993, p. 163). Later in his career, in the late 1960s and early 70s, Zuse made progress in the design of electromechanical prototypes of some components of his ideas (see Sect. 6.3), but in his 1957 paper he sketched out his grand plans for how the technology might be used.
The foundation of Zuse’s vision was the concept of a self-reproducing workshop, made from a sufficient diversity of manufacturing machines so as to achieve closure in the ability for the workshop to manufacture new copies of every machine. We will further discuss the topic of closure in Sect. 7.3.1. We see echoes in Zuse’s approach to Butler’s earlier ideas in Erewhon of the collective reproduction of heterogeneous groups of machines (Sect. 3.1). Zuse saw that such a factory would be able to produce other machines in addition to those from which it was itself comprised; like von Neumann and Moore, he was interested in the possibilities of maker-replicators. This being the case, he said “the question that is of greatest interest is the following: What is the simplest form of initial workshop necessary to crystallize out of it a complete industrial plant?” (Zuse, 1957, p. 163).95 Zuse named this idea, of a minimal self-reproducing seed out of which whole industrial plants for specific purposes could grow, the technical germ-cell.
Pushing the idea further, Zuse imagined that a technical germ-cell like this could be directed to make a copy of itself at a slightly smaller scale, leading to a lineage of germ-cells of progressively smaller size. The result, he envisaged, would be a microscopic germ-cell that was “not only … the constructionally and logically simplest form, but also the smallest in space” (Zuse, 1957, p. 164).96 From this microscopic germ-cell, which Zuse referred to as the “real germ-cell” (Zuse, 1957, p. 164),97 an entire human-scale industrial plant could be manufactured by reversing the sequence of miniaturisation steps through which the real germ-cell had been created. Using this technology, he speculated, future generations of engineers might not build industrial plants and factories but plant them and simply supply them with sufficient raw materials and energy with which to grow. Zuse’s ideas call to mind Philip K. Dick’s image at the end of his short story Autofac of miniature seeds of manufacturing plants being launched into space (Sect. 4.1.3). Dick’s story appeared in 1955, two years before Zuse’s talk. However, comments in Zuse’s handwritten notebooks from 1941 confirm that he had originated the idea independently and had been thinking along these lines for a long time (Zuse, 1941).
Zuse ends the 1957 paper with the thought that the technical germ-cell could also be used to manufacture computing devices, and that this might be a route to evolve artificial intelligence that could eventually be “able to perform … inventions and mathematical developments … better than man” (Zuse, 1957, p. 165).98
Read in isolation, the ideas relating to the technical germ-cell set out in Zuse’s paper appear somewhat far-fetched from an engineering perspective—although perhaps no more so than Moore’s paper from the previous year. Nothing is said about the information and control mechanisms that would be required to drive the processes he discussed. Furthermore, regarding the process of miniaturisation Zuse envisaged to arrive at the “real germ-cell”, he acknowledged that different physical principles and manufacturing methods would be applicable at different physical scales—but simply noted that this would be a significant problem to be tackled in future research (Zuse, 1957, p. 163). However, this was a transcript of a relatively short speech given at an honorary degree ceremony; it was not an occasion to present a long discussion of detailed technicalities. Indeed, at the end of the speech Zuse asks of his audience “Forgive me, please, if I let the imagination play farther than is usual at scientific conferences” (Zuse, 1957, p. 165).99 In later publications it is clear that Zuse had realistic expectations about the timescales and challenges that would be involved, and he was also serious about the enormous significance of its potential long-term applications. In the following decade he wrote at greater length and in more detail about his ideas, and also commenced work on some prototype hardware. We describe these later works in Sect. 6.3.
5.4.3 George R. Price (1957)
Another speculative essay from around the same time is of interest mostly for historical and biographical reasons, rather than for making an original contribution. Presented in the form of a fictional vision, The Maker of Computing Machines was written by George R. Price (1922–1975) and appeared in the pioneering computing magazine Computers and Automation in 1957 (Price, 1957). Price is best known for his contributions to evolutionary theory, yet he worked in various fields in his early career, including a number of years as an IBM employee in the 1960s (Harman, 2010).
The story describes an inventor who creates a series of progressively more complex computing machines—and, later, robots—incorporating mechanisms such as self-repair, goal-based behaviour, associative learning and long-term planning. The advanced robots eventually learn how to make some of the earlier computer designs themselves, but they also acquire some unsavoury behaviours such as torturing and killing their own kind. The inventor had wanted his robots to develop qualities of altruism, benevolence and cooperation, but he found it too difficult to codify these into explicit goals. So he equipped the robots with simple built-in goals such as keeping themselves in repair and seeking fuel, and provided them with a mechanism by which they could develop more complex derived goals by themselves. The more complex goals would enable the robots to achieve their built-in goals in creative ways, based upon their experiences as they explored and learned about their world. However, the unsavoury behaviours that were observed were quite the opposite to the inventor’s intended outcome.
In this short story, Price pinpoints a key issue facing AI designers today: the problem of how to prevent learning systems from developing unwanted behaviours. In present-day debates about the dangers associated with advanced AI this has become known as the value alignment problem (see Sect. 7.3.4). The idea of creating intelligent machines through biologically-inspired learning mechanisms had been discussed by Alfred Marshall ninety years earlier (Sect. 3.2), and the theme of technology out of control had been raised by Samuel Butler at around the same time as Marshall (Sect. 3.1) and by many early twentieth century authors (Sect. 4). Still, Price’s story is an interesting example of a contribution from an early theoretical biologist. In highlighting the difficulties in developing cooperative and altruistic behaviour, it also anticipates Price’s later work in theoretical biology on kin selection.
5.5 Self-Reproduction in the Cybernetics Literature
The late 1940s saw the birth of the scientific field of cybernetics, which sought a common understanding of principles of control and communication in animals and machines. Among those working in the area, there was a common view of intelligence as a search problem, and parallels were drawn between the processes of lifetime learning and evolution. Examples can be found, among others, in W. Ross Ashby’s notion of intelligence amplifiers (Asaro, 2008) and in Alan Turing’s early work on artificial intelligence (Turing, 1950).100 In addition to this general interest in evolution applied to machines, some of the leading cyberneticists specifically discussed the idea of self-reproducing machines. In particular, Norbert Wiener, Gordon Pask and W. Ross Ashby all published work on self-reproduction and evolution in the early 1960s.
Wiener’s influential book Cybernetics, or control and communication in the animal and the machine, first published in 1948, was supplemented with two additional chapters in the 1961 second edition: one of the new chapters was entitled On Learning and Self-Reproducing Machines (Wiener, 1961).101 In this, he discussed the relationship between lifetime learning and evolution; while the majority of the chapter is devoted to lifetime learning systems, in the last few pages Wiener turns to the subject of self-reproduction.102 He describes the design of an example logical self-reproducing system in the form of a particular kind of electronic circuit that could automatically imitate the behaviour of a given second circuit.
However, Wiener’s proposal is not an entirely satisfactory example because the thing that is being reproduced—the behaviour of the given circuit—is not in any way playing an active role in its own reproduction. Although the reproduction process was entirely automated, it relied upon the existence of additional electronic circuitry in order to bring about the reproduction of the reference behaviour. As we have seen in other work described in this chapter, the issue of how much of the process of reproduction should be directed by the self-replicator itself, and how much should rely upon very specific features of its operating environment, was a topic discussed by others researchers of the time, including von Neumann (Sect. 5.1.1), Jacobson (Sect. 5.3.2) and Ashby. We return to discussion of this issue in Sect. 7.3.
Also published in 1961 was Pask’s An Approach to Cybernetics (Pask, 1961), which included a chapter entitled The Evolution and Reproduction of Machines. Pask considered the problems involved in creating artificial evolutionary systems that exhibit on-going, open-ended evolutionary activity; his focus was therefore very much upon the possibilities of evo-replicators. He noted that if, over time, the environment experienced by any one machine becomes increasingly determined by other evolving machines in the system, this will produce an “autocatalytic” effect that avoids the need for the system designer to build a drive for evolutionary trends into the system’s reward structure (Pask, 1961, pp. 101–102). He also argued that the successful evolution of a species of machine in a competitive environment was likely to involve the sequential development of a hierarchy of levels of description (or “metalanguages”) used in its genetic or control structures, with which the machines would encode information about their own design and their relationship with the environment (Pask, 1961, p. 101).103
A somewhat different approach to the subject was taken by W. Ross Ashby in his 1962 paper The Self-Reproducing System (Ashby, 1962). Like Penrose and Jacobson before him, Ashby emphasised that self-reproduction is a function of the interaction between the form that is reproduced and the environment within which the form exists as a subsystem. Considering self-reproduction processes in general, he argued (as did von Neumann and Jacobson) that the allowed complexity of the building blocks is essentially an arbitrary decision. To demonstrate this, he gave a string of examples of real-world systems that fit his basic definition of self-reproduction. In most of these, the form being reproduced is relatively simple, and the process of reproduction is largely due to the particular (complex) environment in which the form exists. One of his more whimsical examples is a yawn, which reproduces in a suitable environment of people. Given this, he argued that it is the particular properties of the terrestrial environment on Earth that distinguish the processes of biological self-reproduction and evolution from these other, less interesting, examples. As we already saw with Wiener’s work, this question of how much of the complexity of the process of reproduction resides within the environment rather than within the self-replicator itself is indeed an important issue, and we return to it in Sect. 7.3. It is also the case that many of the examples of self-reproducing systems offered by Ashby were standard-replicators, which were not capable of heritable mutations as required by von Neumann’s test for “interesting” self-reproduction (Sect. 5.1.1); that is, they were not evo-replicators.
Developments in cybernetics around this period were not confined to the United States and Europe. In the Soviet Union during the early 1950s the field had initially been greeted with scepticism, being regarded by some as a “reactionary pseudoscience” that served the interests of the bourgeoisie by reflecting its desire to “replace potentially revolutionary human beings with machines” (Holloway, 1974, p. 299). By the late 1950s, however, attitudes had changed, as attested to by the establishment in 1959 of a Science Council for Cybernetics by the USSR Academy of Sciences (Holloway, 1974, p. 299).
In 1961, the Russian polymath Andrei Nikolaevich Kolmogorov (1903–1987) presented a well-attended seminar on “Automata and Life” to the Faculty of Mechanics and Mathematics at Moscow State University. In this and two subsequent talks in 1962 he explored the implications of materialism, and of the nascent field of computer science, for our understanding of life and mind. The talks in 1962 were entitled “Life and thinking as special forms of the existence of matter” and “Cybernetics in the study of life and thinking.” Some general information regarding the circumstances of these talks is provided in (Uspensky, 1998, p. 497).
Kolmogorov prepared an extended abstract for Automata and Life, which was later published in various different editions.104 The content of the three lectures also formed the basis of a second paper, Life and thinking as special forms of the existence of matter, which was also published in several different forms.105
In these talks Kolmogorov suggested that the age of space travel brought with it the prospect of encounters with extraterrestrial intelligent beings. This presented a pressing need for understanding the concept of life in more general terms, abstracted from the specific chemical details of life on Earth. Likewise, the advent of the computer age created an urgent need to conceptualise thought and cognition in more general terms.
Kolmogorov opened Automata and Life with three questions:
Can machines reproduce their kind, and in the course of such self-reproduction can progressive evolution take place leading to the creation of machines of a higher degree of perfection than the originals?
Can machines experience emotions?
Can machines have desires and can they pose for themselves new problems not put to them by their constructors?
— A. N. Kolmogorov, Automata and Life, 1961 (Kolmogorov, 1961, p. 3)106
We can see in these questions that his focus was specifically on evo-replicators. In these talks aimed at a wide audience, Kolmogorov did not delve too deeply into technical responses to these topics. However, he did point out that, within the framework of a materialist worldview, it must be admitted that there are no fundamental arguments against a positive answer to these questions (Kolmogorov, 1964, p. 53). In other words, if biological organisms can do these things, then it should, in principle, be possible for machines to do them too.
Kolmogorov cautioned that the current cybernetics literature displayed both many exaggerations and many simplifications (Kolmogorov, 1968, p. 25). Furthermore, he observed that research on understanding human behaviour was focused on the most simple conditioned reflexes, on the one hand, and on formal logic, on the other hand (Kolmogorov, 1968, pp. 27–28). The vast space between these two extremes in understanding the architecture of human behaviour, Kolmogorov noted, was not being studied in cybernetics at all. Hence, he suggested, the kind of developments he was discussing may take longer to come to fruition than many people might expect.
Taking early attempts at musical composition by computers as a specific example, Kolmogorov warned that in order to properly simulate or build living beings, we need to understand the source of their internal desires and not just purely external factors; to design a computer that can generate interesting music, we need to understand the difference between living beings in need of music and beings who do not need it (Kolmogorov, 1968, p. 26). Having argued that we could, in theory, fully understand our own design principles, Kolmogorov suggested that we should not be afraid of creating automata that imitate our own abilities (Kolmogorov, 1968, p. 31) or, indeed, of creating automata just as highly organized but very different from us (Kolmogorov, 1968, p. 15). Rather, we should take great satisfaction in the fact that the human race has developed to the point where we can create “such complex and beautiful things” (Kolmogorov, 1968, p. 31).
It is interesting to note the parallels between Kolmogorov’s thoughts in this article and those of Ada Lovelace in her comments on Charles Babbage’s Analytical Engine, written over a century earlier in 1843.107 As Kolmogorov cautioned against hype in the promise of cybernetics, so too had Lovelace cautioned against “exaggerated ideas that might arise as to the powers of the Analytical Engine” (Menabrea, 1843, p. 722). However, Lovelace had gone on to state that the “Analytical Engine has no pretensions whatever to originate anything. It can do whatever we know how to order it to perform” (Menabrea, 1843, p. 722) (original emphasis). In contrast, in answering his third question in the affirmative, Kolmogorov had suggested that it should, in principle, be possible to build machines that can originate new goals. Finally, Lovelace famously suggested that “the engine might compose elaborate and scientific pieces of music of any degree of complexity or extent” (but only if “the fundamental relations of pitched sounds in the science of harmony and of musical composition” could be codified into a suitable sequence of operations) (Menabrea, 1843, p. 694). As previously stated, Kolmogorov was less interested by the prospect of the purely algorithmic generation of music, and wanted instead to understand the design principles that instil human beings with the desire to compose music. We will return to the topic of how machines might develop their own purposiveness and internal desires in Sect. 7.3.4.
* * *
To summarise what we have discussed in this chapter, the 1950s witnessed the attainment of the third and final step in the historical development of the idea of self-replicator technology (Sect. 1.6)—the arrival of the first examples of actual implementations of self-replicators, both in software and in hardware. As we have seen, this was accompanied by the emergence of a new concept: the use of self-replicator technology in the design of universal manufacturing machines, i.e. maker-replicators.108 Having covered the attainment of the three major steps in the development of thinking about self-replicator technology, in the next chapter we present a brief review of more recent developments with standard-replicators, evo-replicators and maker-replicators, from the 1960s to the present day.
References
In Chap. 6 we provide references to the most significant of these other reviews.↩︎
See (McMullin, 2000) for an insightful discussion.↩︎
Subsequent authors have also discussed the connection between von Neumann’s design and Kleene’s Recursion Theorem (see, e.g., (Case, 1974, pp. 28–29), (Kampis, 1991, pp. 367–371)).↩︎
Von Neumann’s description of the logical design of a self-reproducing machine can equally be applied to the reproductive apparatus of biological cells. However, although his work pre-dated the unravelling of the details of DNA replication by some years, it had little impact on developments in genetics and molecular biology (Brenner, 2001, pp. 32–36).↩︎
Arthur W. Burks, who edited von Neumann’s posthumously published book Theory of Self-Reproducing Automata, commented that von Neumann “intended to disregard the fuel and energy problem in his first design attempt. He planned to consider it later” (von Neumann, 1966, p. 82).↩︎
The cellular model was based upon a Cellular Automaton (CA) design, which von Neumann had conceived with his colleague Stanislaw Ulam, and is the first work to use the now-popular CA formalism. Von Neumann had originally conceived of a more complex “kinematic model”, but Ulam observed that a discrete model would be more analytically tractable (Aspray & Burks, 1987, p. 375). In Ulam’s biography, he himself recalls informal discussions that he had with Stanislaw Mazur of the Lwów Polytechnic Institute in 1929 or 1930 on “the question of the existence of automata which would be able to replicate themselves, given a supply of some inert material” (Ulam, 1976, p. 32).↩︎
By arrangement with von Neumann (von Neumann, 1966, p. 95), Kemeny’s article (Kemeny, 1955) was based upon lectures that von Neumann had delivered at Princeton University in 1953 and upon parts of the manuscript for (von Neumann, 1966).↩︎
As mentioned in Sect. 1.4, the study of open-ended evolutionary systems has attracted significant renewed interest within the Artificial Life and AI communities within the last few years (T. Taylor, Bedau, et al., 2016), (Stanley et al., 2017), (Packard et al., 2019). See Sect. 6.1 for further discussion of this topic.↩︎
Furthermore, in 1963 he proposed early ideas for what is now known as DNA computing (Barricelli, 1963, pp. 121–122). In recent years, Barricelli’s work has started to receive slightly more coverage in the academic literature (e.g. (Fogel, 2006), (Galloway, 2012)), in books (e.g. (G. Dyson, 1997), (G. Dyson, 2012)) and in magazine articles (e.g. (Galloway, 2011), (Hackett, 2014)).↩︎
Sources of biographical details in this paragraph and the next include (G. Dyson, 2012, pp. 225–228) and (Galloway, 2012, pp. 29–31).↩︎
The design was a kind of one-dimensional cellular automaton (see earlier footnote in this section), considerably simpler than the two-dimensional CA employed in von Neumann’s cellular model. In the experiments Barricelli conducted at IAS, the world was a cyclic array with 512 squares, where the state of each square could lie in the range -40 to +40 (The Staff, Electronic Computer Project, 1954, pp. II–83).↩︎
Barricelli’s first results were published, in Italian, in the journal Methodos in 1954 (Barricelli, 1954), followed in 1957 by an expanded English-language version in the same journal (Barricelli, 1957). The most detailed presentation of his work appeared in two papers published in the theoretical biology journal Acta Biotheoretica in 1962–63 (Barricelli, 1962), (Barricelli, 1963), with a more condensed summary in The Journal of Statistical Computation and Simulation in 1972 (Barricelli, 1972).↩︎
Symbioorganisms can be viewed as examples of what have now become known as collectively autocatalytic sets (see, e.g., (Kauffman, 1986)).↩︎
Barricelli initially came up against the problem of the system reaching a state of “organized homogeneity” after a few hundred generations (Barricelli, 1962, p. 88). This occurred when a single variety of symbioorganism had invaded the whole world and no further change was observed. He made several attempts to avoid this behaviour, and finally adopted a successful approach that involved two modifications to the original design. First, he divided the world into four separate areas and used slightly different update rules in each area, and second, he ran several different evolution experiments in parallel, exchanging the content of subsections of the world between two universes every 200 or 500 generations (Barricelli, 1962, p. 89). The topic of diversity maintenance in computational evolutionary systems is still very much a matter of active research (Črepinšek et al., 2013).↩︎
Barricelli clarified his use of biological terminology at the start of the paper, justifying his use of such terms because they “were easy to remember and [they made] analogies with biological concepts immediately clear to the reader without requiring tedious explanations.” However, he cautioned that “[t]he terms and concepts used in connection with symbioorganisms are in no case identical to biological concepts; they are mathematical concepts …” (Barricelli, 1962, p. 70).↩︎
Although he reported that in the latter stages of the runs “evolution proceeded at a slower rate until generation 5000 when the experiment was discontinued” (Barricelli, 1962, p. 90).↩︎
This allowed Barricelli to use worlds of size 3072 locations—almost a six-fold increase compared to the experiments on the IAS Machine.↩︎
This game was described by Martin Gardner and based upon the popular game of Nim (Gardner, 1958).↩︎
Barricelli used “the number of correct final decisions of the winner” as the measure of skill level, and reports that human novice players typically show a skill-level of 1 or 2 in their first five games played (Barricelli, 1963, p. 107).↩︎
See (Barricelli, 1963, pp. 114–116) for details. Barricelli summarises that “the parasite never developed an independent game strategy to any degree of efficiency and was entirely dependent on its host organism for game competitions with, and transmission of the infection to, uninfected hosts” (Barricelli, 1963, p. 125). In one line of subsequent research, he worked with colleagues on a quite different evolutionary system more resembling a genetic algorithm, and obtained better results in evolving strategies for poker (Reed et al., 1967), (Barricelli, 1972, pp. 119–122).↩︎
He had already discussed the importance of membrane structures in the early evolution of biological life in his 1963 paper (Barricelli, 1963, pp. 123–124).↩︎
The paper would have made an excellent addition to the inaugural Interdisciplinary Workshop on the Synthesis and Simulation of Living Systems (the original precursor of the current Artificial Life conference series) held in Los Alamos, NM in the same year, 1987. Sadly, Barricelli did not attend the workshop.↩︎
The first of these was a brief letter co-authored by Penrose’s son, the now-eminent physicist Roger Penrose (Penrose & Penrose, 1957). The later publications were more extensive, and authored by Lionel Penrose alone (Penrose, 1958), (Penrose, 1959). The Wellcome Library in London has a treasure trove of notes, correspondence, photographs, etc. relating to Penrose’s research, freely available in digitised form at https://wellcomelibrary.org/item/b20218904 (the physical items are held in the nearby UCL Library Special Collections archive). Items from the archive are categorised hierarchically, with all of the work on self-reproduction filed under reference PENROSE/2/12/x. In the following footnotes, any references of this form can be found by navigating from the URL given above.↩︎
Of course, anyone considering the use of models of this type to explore the origin of life would have to relax this restriction.↩︎
Penrose did not refer to Barricelli’s work in his papers, although he did become aware of it at some stage—the Penrose collection at the Wellcome Library includes a copy of a technical report that Barricelli had published in 1959 (Barricelli, 1959) (PENROSE/2/12/17/11; see earlier footnote in this section).↩︎
PENROSE/2/12/14 (see earlier footnote in this section). At the time of writing, several versions of the films can be found online. Links to these can be found at https://www.tim-taylor.com/selfrepbook/.↩︎
E.g. PENROSE/2/12/2, PENROSE/2/12/3, PENROSE/2/12/4, PENROSE/2/12/12 (see earlier footnote in this section).↩︎
PENROSE/2/12/9 (see earlier footnote in this section). Other highlights of the episode included the pioneering molecular biologist Sydney Brenner discussing the genetic code, and Harold Urey describing his work with Stanley Miller on early terrestrial chemistry and the origins of life.↩︎
PENROSE/2/12/11 (see earlier footnote in this section). From the full PDF file available to download from this page, see especially pp. 100–108, 117–140, 174, 177.↩︎
Jacobson also mentioned the possibility of mutations arising in the genetic instructions, although he did not explore the evolutionary implications of this at any length (Jacobson, 1958, p. 274).↩︎
Jacobson also remarked that a different model of self-reproduction could be built into an entirely electronic system (i.e. logical rather than physical self-reproduction). Interestingly, he cited Barricelli in the paper, although the cited papers related to Barricelli’s speculations on the role of gene symbiosis in the origins of modern life. There is no indication that Jacobson was aware of Barricelli’s work on software-based self-reproduction and evolution. He did not refer to Penrose’s work in his paper either, although the two certainly corresponded later on—the Penrose collection at the Wellcome Library includes an offprint of Jacobson’s paper with the handwritten note “Best regards, Homer Jacobson” on the front cover (PENROSE/2/12/17/8).↩︎
In 1955, Jacobson had published a paper on the application of information theory to aspects of reproduction and the origins of life (Jacobson, 1955). In it he referred to mechanical models of reproduction, explicitly mentioning those “conceived, in rather abstract terms, by von Neumann” (Jacobson, 1955, p. 122), and also a “specific and simple model” designed by himself—details of which he said would be reported elsewhere. This is presumably the model described above and reported in (Jacobson, 1958). Interestingly, Jacobson and his 1955 paper were recently in the news when, in 2007 (over half a century after its original publication), he decided to retract two brief passages which he had come to view as unfounded or mistaken, and which had become much cited by creationists as evidence for the impossibility of life arising by accident (see (Jacobson, 2007) for the retraction and (Dean, 2007) for coverage of the story in the New York Times).↩︎
The date of Zuse’s presentation was confirmed by staff at the University Archives of the Technical University of Berlin [personal communication to TT, 14 August 2018].↩︎
Quotation translated by TT from the original German text: “Die Frage, welche dann von größtem Interesse ist, ist folgende: Welche einfachste Form einer Anfangswerkstatt ist erforderlich, um aus ihr ein vollständiges Industriewerk auskristallisieren zu lassen?” (Zuse, 1957, p. 163).↩︎
“nicht nur, die konstruktiv und logisch einfachste Form … sondern auch die räumlich kleinste” (Zuse, 1957, p. 164).↩︎
“die echte Keimzelle” (Zuse, 1957, p. 164).↩︎
“Erfindungen und mathematischen Entwicklungen besser durchzuführen als der Mensch” (Zuse, 1957, p. 165).↩︎
“Verzeihen Sie mir bitte, wenn ich heute einmal die Phantasie etwas weiter habe spielen lassen, als es sonst auf wissenschaftlichen Tagungen üblich ist” (Zuse, 1957, p. 165).↩︎
Turing’s first published thoughts on the idea of evolution as a search process in the context of machine learning appeared in a 1948 research report entitled Intelligent Machinery (Turing, 1948, p. 18). The director of his laboratory at the time was none other than Sir Charles Galton Darwin, grandson of Charles Darwin. He was unimpressed by Turing’s report, dismissing it as a “schoolboy essay” (Copeland & Proudfoot, 1999).↩︎
Burks states that Wiener and von Neumann interacted when developing their respective conceptions of cybernetics and the theory of automata (Aspray & Burks, 1987, p. 364).↩︎
In these last few pages Wiener uses the term self-propagation rather than self-reproduction, in contrast to his use of the latter term in the opening pages of the chapter and indeed in the chapter title.↩︎
It first appeared in 1961 in (Kolmogorov, 1961) (in Russian). An English translation of this article was produced by the U.S. Department of Commerce’s Joint Publications Research Service the following year (Kolmogorov, 1962). Some of the later Russian versions were prepared and edited by Natalya Grigorevna Khimchenko (née Rychkova)—who worked in Kolmogorov’s research group in the early 1960s—to make them suitable for a wider audience. Useful information on the various versions of the talk material, and the differences between them, is provided by Khimchenko at http://vivovoco.astronet.ru/VV/PAPERS/BIO/KOLMOGOR/KOL_REP.HTM (in Russian).↩︎
Quotations from Life and thinking as special forms of the existence of matter provided in this chapter are based upon the original version published in 1964 (Kolmogorov, 1964) (in Russian), with English translation by TT aided by Google Translate. An English translation based upon a later version (Kolmogorov, 1972) was published by NASA (Kolmogorov, 1975), although this is somewhat abridged compared to the original version.↩︎
English translation from (Kolmogorov, 1962, p. 1). According to Natalya Khimchenko, the original talk abstract prepared by Kolmogorov phrased the second question as “Can machines think and experience emotions?” (see website listed in the previous but one footnote). In a later version of the text that appeared in the 1968 publication Кибернетика ожидаемая и кибернетика неожиданная (Cybernetics Expected and Cybernetics Unexpected), the questions are stated as follows: “Can machines reproduce their own kind, and can there be a progressive evolution in the process of such self-reproduction, leading to the creation of machines that are significantly more advanced than the originals? Can machines experience emotions: rejoice, be sad, be dissatisfied with something, want something? Finally, can machines set themselves tasks not assigned to them by their designers?” (Kolmogorov, 1968, p. 14) (English translation by TT aided by Google Translate).↩︎
We met Babbage and Lovelace briefly at the start of Chap. 3.↩︎
In addition to the work of von Neumann, Moore, Zuse and others described in this chapter, the idea of a maker-replicator was also present in some of the later sci-fi stories we mentioned in Sect. 4.1.3, including Philip K. Dick’s Autofac (1953) and Robert Sheckley’s The Necessary Thing (1955).↩︎