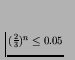 ,
i.e.
,
i.e.
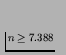 ,
or, in round figures,
,
or, in round figures,
Significant differences were found between runs for five of the measures investigated, at least when using the raw data. These measures were: Program Length, Replication Period, Cumulative Activity, Mean Cumulative Activity, and Diversity.
For Program Length and Replication Period, significant differences (at the 0.05 level) were observed in the raw data values between some runs. For these measures, the mean number of runs that each run is significantly different from at this level was calculated as 12.3 for Program Length and 10.2 for Replication Period, but the high criterion differential on these scores suggests that the true value should be somewhat lower (looking at Figures 6.6 and 6.7, probably somewhere in the range of 6 to 10).
Looking at the derived measures suggested by Bedau and colleagues (i.e. Cumulative Activity, Mean Cumulative Activity and Diversity), significant differences were found between runs which did hold up even at the 0.001 level. Again, the true value of each of these differences probably lay in the range of roughly 6 to 10.
These results indicate that each run, on average, performed
significantly differently to between a third and a half of the other
runs.
One of the main reasons for doing these
experiments was to understand how we should deal with contingency when
conducting further experiments with Cosmos. If we assume that at least
the finding that each run is statistically different to more than a third of
the others is a general result, then we can use the following rule of
thumb: For each re-run of a trial with a different seed for the RNG,
the probability of its outcome being statistically equivalent (at the p=
0.05 level) to the original one is, at most, about
![]() .
Therefore, the
number of re-runs that should be conducted to be confident (at
the 95% level) of at least seeing one statistically different type of
behaviour is n, where
.
Therefore, the
number of re-runs that should be conducted to be confident (at
the 95% level) of at least seeing one statistically different type of
behaviour is n, where
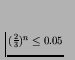 ,
i.e.
,
i.e.
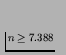 ,
or, in round figures,
,
or, in round figures, ![]() .
This is the
number of re-runs after the original, so, finally, we
can say that any trial should be conducted nine times with different
seeds for the RNG.
.
This is the
number of re-runs after the original, so, finally, we
can say that any trial should be conducted nine times with different
seeds for the RNG.
Having said that each run performed significantly differently to at least a third of the other runs, precisely which runs were significantly different depended upon the particular measure being looked at. This emphasises the fact that one should be clear about exactly what measure is being used when talking about comparisons between evolutionary runs.
The fact that no significant differences were found between any of the runs for any of the measures when looking at differenced sample data suggests that the significant differences observed in raw sample data may be caused (at least in part) by the cumulative magnification of initially small differences as a run proceeds. If this effect is controlled for (which was the purpose of using differenced data), the behaviour of the runs in terms of the change in values of the measures over a given time period would seem to be very similar in all of the runs. However, because of the cumulative magnification of small differences, the absolute outcomes of the runs do differ significantly in some cases, so contingency does play a big role.
As an aside, we can ask to what extent these results can be generalised to other evolutionary systems. Considering biological evolution first, it is clear that even just in terms of population size and the length of runs, the system is completely trivial. Also, the role of contingency may be different in systems which have rich ecological interactions (of which Cosmos programs have very little). It would therefore be unwise to claim that these results can tell us much about the role of contingency in biological evolution, but they may be relevant in specific cases. As for other artificial evolutionary systems, Cosmos is of comparable design, so the results, and the rule of thumb about the number of trials that should be run, should be broadly applicable to these platforms as well. The extent to which ecological interactions affect the results may be investigated by running similar trials on systems that display stronger interactions of this kind (such as Tierra).
In the remainder of this chapter, we will look at the effects of changing various parameter values on the behaviour of the system. In light of the results reported in this section, each of the following experiments is conducted nine times, using different seeds for the RNG each time.