where
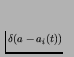 is the Dirac delta function, equal to one
if
a=ai(t) and zero otherwise. Thus, C(t,a) indicates the
number of [genotypes] with activity a at time t.'' [Bedau et al. 98]
is the Dirac delta function, equal to one
if
a=ai(t) and zero otherwise. Thus, C(t,a) indicates the
number of [genotypes] with activity a at time t.'' [Bedau et al. 98]
In biological systems, the fundamental units of evolution are the (L-)genes, and it does not necessarily follow that the evolution of whole organisms will follow this pattern. For example, evolution of an L-gene towards increased L-fecundity across a group of organisms carrying an A-gene instance of the L-gene does not necessarily entail increased A-fecundity of all of the organisms (or A-genes). In Cosmos and similar systems, however, each program as a whole is an encoding of a self-replication algorithm. As such, it can only replicate as a whole; the subsections of a program are highly epistatic, so evolution cannot in general vary one part of the program independently of other parts while retaining the functionality of the whole. Furthermore, replication is asexual, so there is generally no exchange of genetic material between individuals when an offspring is produced. It is therefore reasonable, at least to a first approximation, to treat the whole program as a single A-gene and to expect programs as a whole to evolve along these three axes as described above.
A number of measures were therefore chosen to track changes in each of these three factors through an evolutionary run. The plotting technique used for each of these measures was as follows: for time slice windows of equal width from the start to the end of the run, we plotted the value of the measure for programs that died within that time slice window. For the plots for all three of these factors the data is pruned by only plotting values for individual programs of types which achieved a concentration of at least five individuals at some time during the run (as determined by the parameter species_count_threshold_for_recording). The data was further pruned by only recording information for 1 in every 50 eligible programs (as determined by the parameter morgue_record_period). In the plots, the darkness displayed at any point reflects the number of individual programs taking that particular value at that particular time (i.e. the more programs, the darker the plot).
For A-longevity, we looked at the age at death of each program. An example plot can be seen in Figure 5.7.
For A-fecundity, we looked at two measures: the number of time slices between the first and second successful replication of each program (the replication period) (this could obviously only be applied to programs that successfully replicated at least twice in their lifetime), and the length of programs. The length of a program is an indirect measure of fecundity--all things being equal, a longer program will take longer to replicate than a shorter program, as the longer one has to copy more instructions. An example plot for replication period can be seen in Figure 5.4, and for length, in Figure 5.2.
For A-fidelity, we looked at two measures: the flaw rate,5.2 and the proportion of the total number of offspring produced by an individual that were unfaithful (i.e. less than 100% accurate). Example plots of these two measures can be seen in Figures 5.6 and 5.11 respectively.
In addition to the measures of A-longevity, A-fecundity and A-fidelity, we also used a visualisation technique developed by Mark Bedau and colleagues [Bedau & Brown 97]. The fundamental idea behind this technique is:
``to identify those genotypes[5.3]that make a difference in the evolutionary process. Generally, we consider a genotype to `make a difference' if it continues to be active in the evolving system... In [Tierra-like models] the relative adaptive significance of a genotype is reflected by its concentration in the population. Relatively well adapted genotypes will have a relatively high concentration in the population, and relatively poorly adapted genotypes will we correspondingly scarce. Thus, we here define the [cumulative evolutionary activity counter] ai(t) of the ithgenotype at time t as its concentration integrated over the time period from its origin up to t, provided it exists:To summarise the evolutionary activity of all the genotypes throughout the history of evolution in the system, we proceed as follows:
where ci(t) is the concentration of the ith genotype at t. A genotype's [cumulative evolutionary activity counter] reflects its adaptedness (relative to the other genotypes in the population) throughout its history in the system.'' [Bedau & Brown 97]5.4
``The values of the activity counters of each [genotype] in the system over all time can be collected in the component activity distribution, C(t,a), as follows:
whereis the Dirac delta function, equal to one if a=ai(t) and zero otherwise. Thus, C(t,a) indicates the number of [genotypes] with activity a at time t.'' [Bedau et al. 98]
The visualisation technique is simply to graph these component activity distribution functions. This can be simplified by just plotting a point in (t,a) space whenever C(t,a) > 0.
These activity distribution functions (also referred to as ``activity wave diagrams'') provide a concise visual record of the appearance, competition and death of genotypes throughout an evolutionary run. Bedau and Brown also discuss how they can be interpreted in more detail, to reveal features such as periods of random drift among selectively neutral variants [Bedau & Brown 97]. Example activity wave diagrams can be seen in Figures 5.13-5.15.
The activity wave diagrams indicate which genotypes played important roles during the evolutionary run. The final individual-based analysis technique we used was to actually look at the code of significant genotypes, and to make comparisons between them. In particular, by looking at the genotypes which were abundant at the end of a run and comparing them to the genotype of the ancestor, we can get some idea of which parts of the ancestor were vital for its reproductive success (and therefore were more or less unchanged at the end of the run), and which parts were more redundant or less efficient (and how evolution managed to improve them).